
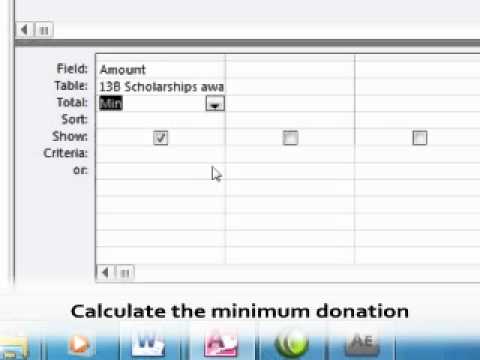
In the final columns, some of that variation can also be attributed to interaction between subjects and either rows or columns. The SS for residual is smaller when you assume repeated measures, as some of that variation can be attributed to variation among subjects.The SS values for the interaction and for the systematic effects of rows and columns (the top three rows) are the same in all four analyses.
This measures the total variation among the 18 values. Now look at the SS columns for the analyses of the same data but with various assumptions about repeated measures.
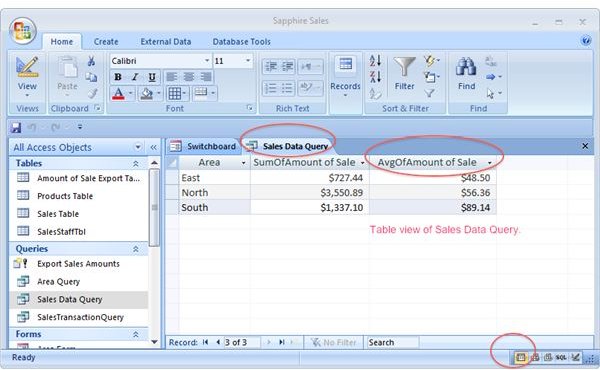
In a query statistical calculations are what how to#
How to report two-way ANOVA results in a table Sum-of-squaresįocus first on the sum-of-squares (SS) column with no repeated measures: I rearranged and renamed a bit so the four can be shown on one table ( Excel file). Here are the ANOVA tables for the four conditions. The colors are repeated between tables, but this means nothing. Each color within a table represents one subject. The tables below are color coded to explain these designs. I analyzed the data four ways: assuming no repeated measures, assuming repeated measures with matched values stacked, assuming repeated measures with matched values spread across a row, and with repeated measures in both directions. I entered data with two rows, three columns, and three side-by-side replicates per cell. But if you are curious in the details, this page explains how the ANOVA table is calculated. You can interpret the results of two-way ANOVA by looking at the P values, and especially at multiple comparisons.


 0 kommentar(er)
0 kommentar(er)
